How to Calculate Resonance
December 20, 2022
Since developing AcousticGender.space, a lot of people have asked me how the resonance calculation works.
The brief explanation is that the system finds the formants in each vowel sound. Then it measures how high or low they are compared to the average for that vowel. The higher they are, the higher the resonance score, with with F₁ counting for about three times as much as F₂ and F₃ counting for little-to-nothing.
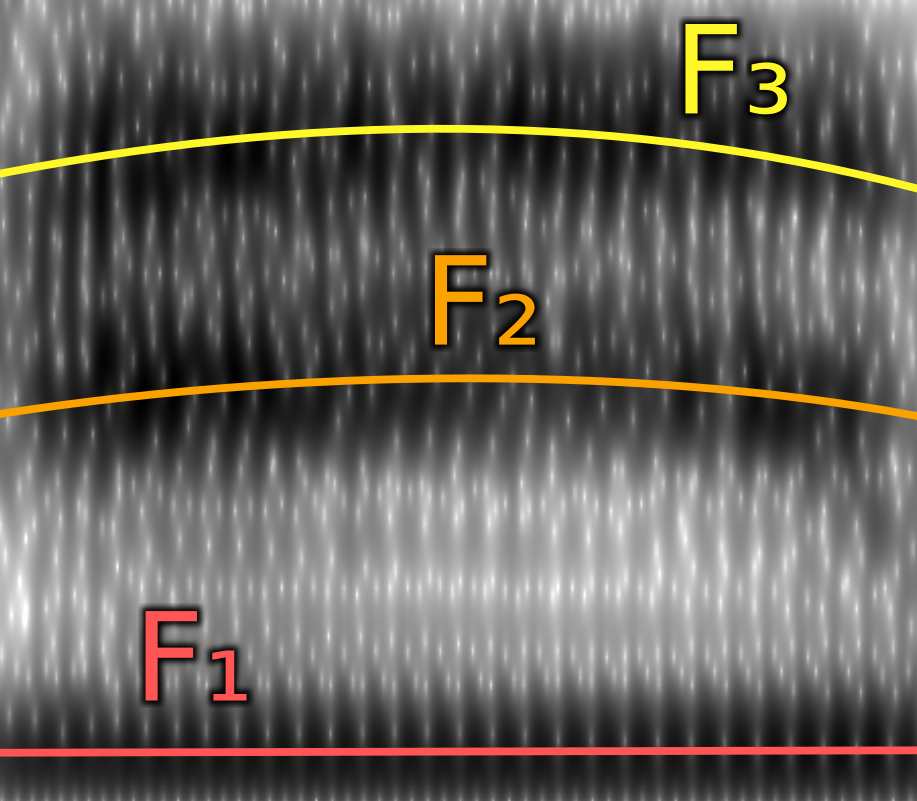
Formants are bands of concentrated energy in the sound spectrum. They’re created by sound waves bouncing around as they move through a passage, such as a vocal tract. The smaller the psasage, the more they bounce around and the higher the frequency. The base frequency of the sound is called F₀, or pitch. The first formant above F₀ is called F₁, the second is called F₂, etc.
For my Master’s project, I wrote a formal definition with math that looks like this:
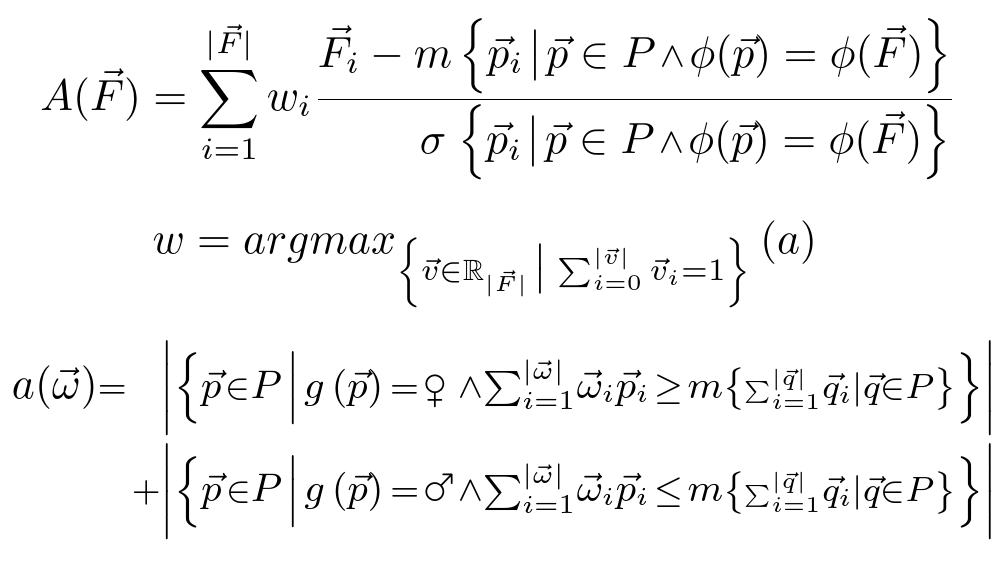
However, the notation makes it look way more complicated than it actually is. It’s really just high school-level statistics.
Walking through an example, in the “please call Stella” example recording, the formant frequencies you get from Praat for the “a” in “call” (= /ɔ/) were
F₁: 620Hz
F₂: 1077Hz
F₃: 3079HzGiven that, can we find how far above or below the average for an /ɔ/ each of those values are. The unit we use is standard deviations (σ).
F₁: 620Hz vs average 612Hz = 0.053σ = just barely above average for an /ɔ/
F₂: 1077Hz vs average 1097Hz = -0.042σ = just barely below average for an /ɔ/
F₃: 3079Hz vs average 2522Hz = 1.234σ = above average for an /ɔ/Now, each of the three formants aren’t equally significant to how we perceive gendered resonance. So we have to multiply each normalized frequency by a certain a certain constant “weight”. The set of weights that that most accurately distinguished between male and female recordings in a sample dataset was:
F₁: 0.732
F₂: 0.268
F₃: 0.000So the weighted average is
0.732 × 0.053
+ 0.236 × -0.042
+ 0.000 × 1.234
= 0.027I didn’t realize in advance that the weight for F₃ would be zero, so it could also be considered a weighted average of just F₁ and F₂. However, using different data or outlier removal schemes can change this so that F₃ has a small but non-zero value, so who knows.
Now, the number 0.027 is on a scale where 0 is the average, 1 is moderately above average, and 2 is far above average. For below average, it’s the same but the numbers are negative. So at 0.027, the resonance in this recording is slightly above average. Technically we can stop there, but I thought people would find it easier to think of 50% as the average, 75% as above average, and 100% as far above average. For that to be the case, we just add 2 to each result, then divide by 4 and multiply by a hundred.
(0 + 2) / 4 × 100 = 1/2 × 100 = 50%
(1 + 2) / 4 × 100 = 3/4 × 100 = 75%
(2 + 2) / 4 × 100 = 4/4 × 100 = 100%So, the percentage for 0.027 is:
(0.027 + 2) / 4 × 100 = 50.68%.That’s for a single syllable. When you’re not playing back a clip, the application shows you the median resonance across every syllable – that’s typically what you want to focus on, especially when starting out.
